Not many are aware that the mathematical theory of the ET scale was first published by Chu Tsai-Yu in China during the days of the Ming Dynasty in 1584.
In those days, there used to be a lot of trade between Europe and China. In 1636, i.e, barely 52 years later, Simon Stevin and Marin Mersenne wrote about ET scale in Europe.
The Ming Dynasty ended in 1592, however, Chu's publication was to change the world's music forever. ET scale was used first in Germany in 1690 and the Organ in Newcastle-upon-Tyne at the St.Nicholas Church was the first to be tuned to ET scale in 1842.
Each note in the ET scale is at a distance of a multiple of 1.0594631 from the previous note.
The tuning of the keyboards of Pianos, Organs, Accordions, and Harmoniums is done in this manner.
This magic number is the "12th root of 2".
This means that when any number is multiplied by this magic number 12 times, the original number will be doubled. (Refer to following table)
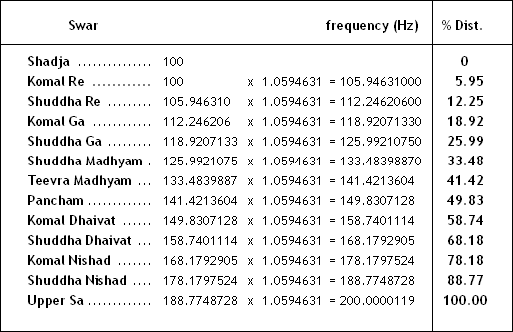
Table shows % distances of every note in Octave (Saptak) as per 12-Tone-Equitempered (ET) Scale (as tuned in Pianos, Synthesizers, Keyboards, Organs, Harmoniums, Accordions)
Remember : Multiply Hz frequency of any key by 1.0594631 to get the frequency of next key;
and divide to get the frequency of the previous key.
From S
Take any starting key as S = say 100 Hz
Note : All the 12 notes in the Equitempered Scale are "Unnatural".
Practical Example : Komal Dhaivat of 'A' or Saphet 6 is 'F'. 'A' is 440 Hz. F will be at a distance of Komal Dhaivat i.e., at 58.74%. 440 x 58.74% + = 698.456 Hz.
In ET scale, if we listen to the Shadja and Gandhar (played together) in any key taken as the Shadja, we find that there is no consonance.
This is because, the S-G distance in the tempered scale is almost 26% whereas the Natural S-G distance as heard on a Tanpura is a pure 25%. S-P distance in tempered scale is 49.83% whereas the Natural S-P distance as heard on a Tanpura is a pure 50%.
Similarly, there are differences in all other notes between the ET scale and the Natural scale.
